[Generative Artificial Intelligence] Normalizing Flow Models – 1

Stanford CS236 Deep Generative Models 수업의 자료를 기반으로 생성모델의 기본 개념들을 정리해보고자 한다. (참고 https://deepgenerativemodels.github.io/syllabus.html)

이전의 latent variable model은 이미지의 특징을 담은 z를 만들어 사용해서 p(x|z)를 통해 확률분포를 만들었고 p(x|z)가 간단한 가우시안 분포여도 p(x)는 복잡한 분포를 표현할수 있었다. 하지만 여기서 p(x)를 계산하는것이 모든 z에 대해 계산을 해야해서 intractable해지고 likelihood를 구하기 어려웠다. 이러한 p(x)를 tractable하게 만들고자 하는것이 중요한 이슈가 된다.

그래서 나오는 flow model의 key idea는 z의 분포를 단순한 분포(gaussian, uniform등)으로 정하고 단순한 분포로부터 복잡한 분포로 mapping을 하는데 이를 mapping과정을 invertible하게 만드는것이다. 이렇게 하면 p(x)의 likelihood 계산 과정이 용이해진다고 한다.

결론부터 얘기하면 아래와 같이 invertible한 \( f_\theta \) 함수를 만들어 p(x)를 계산하게 된다.

위와 같은 식이 나오는 이유는 아래의 change of variable의 원리에 따라 나오는 것이다. 아래는 1D case인데 이걸 고차원으로 확장하면 위와 같은 식으로 p(x)를 구할 수 있게 된다.

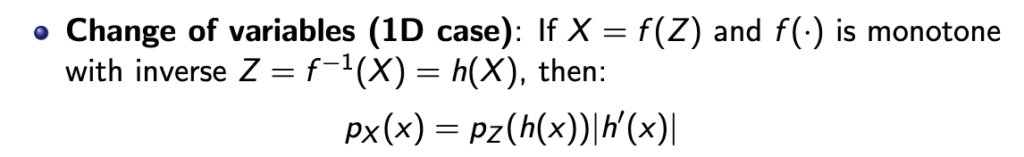
위에서는 z에서 x로 매핑이 한번에 되는것처럼 나오긴 했는데 실제로는 이 단계를 쪼개서 여러번 매핑을 하게 된다. 그래도 아래처럼 똑같이 표현이 가능하다.

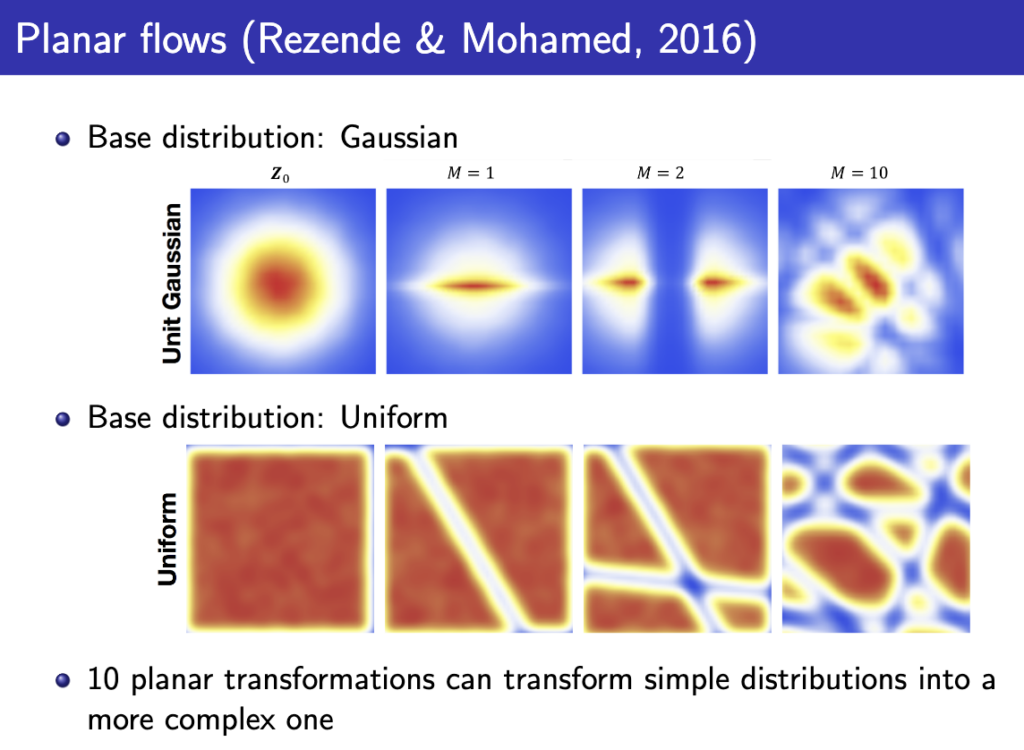
그렇게 위 식에서 \( \theta \)를 잘 학습시키면 아래와 같이 simple한 z에서 시작해서 점점 복잡한 x로 변환되는 과정을 볼 수 있다.

이 \( \theta \)를 학습시키는건 계속 해왔듯이 maximum likelihood를 구해서 학습시키게 되고 maximum likelihood를 구하는 식은 아래와 같다.

여기서 maximum likelihood를 계산하기 위해 몇가지 조건이 필요한데,

1. p(z)가 sampling이 쉽고 likelihood가 tractable해야한다. (ex. 가우시안 분포)
2. f가 invertible해야한다.(likelihood계산에서는 x->z mapping을 쓰고 sampling에서는 z->x mapping을 사용)
3. f의 jacobian계산이 용이해야한다. – n x n 행렬의 jacobian을 구하는 complexity는 \( O(n^{3}) \)여서 매우 커 계산이 힘들다. 이때 아래처럼 특정 조건을 걸면 jacobian계산을 linear로 바꿀 수 있다.