[Generative Artificial Intelligence] Score Based Models – 1

Stanford CS236 Deep Generative Models 수업의 자료를 기반으로 생성모델의 기본 개념들을 정리해보고자 한다. (참고 https://deepgenerativemodels.github.io/syllabus.html)

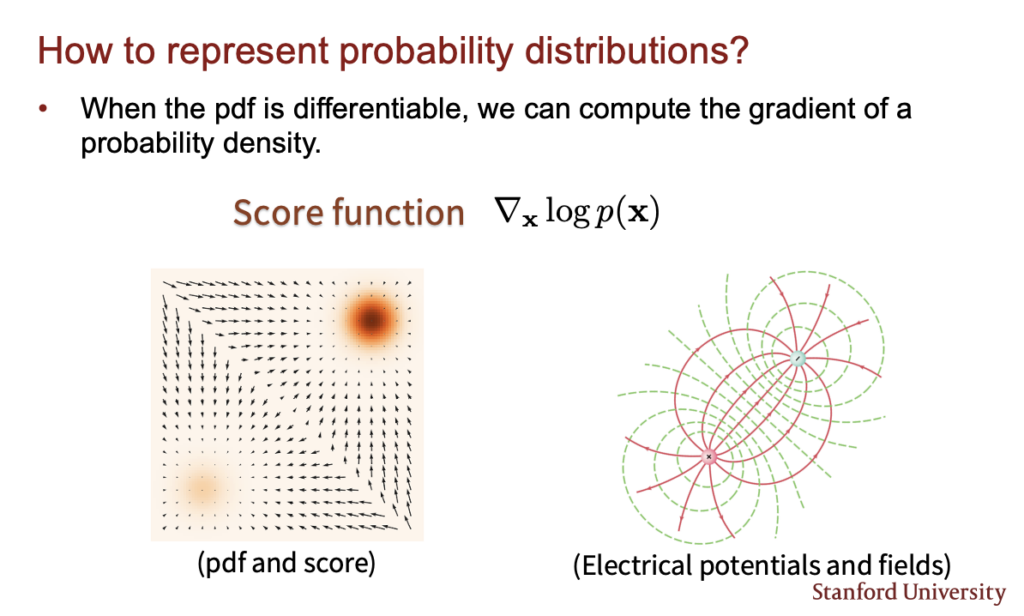
지금까지 다룬 Autoregressive model, Normalizing Flow model, GAN, Energy based model등은 다양한 방식으로 데이터의 확률분포를 표현하고 그러한 확률분포가 실제 데이터의 분포와 유사해지도록 학습된다. 이번 lecture에서 다룰 score based model은 데이터의 확률분포를 직접 배우는것이 아니라 기울기를 나타내는 score (\( \nabla _x log p_\theta(x)\))를 배우고 그 score를 통해 데이터를 생성한다. 아래 왼쪽 그림은 데이터의 확률분포와 그 score를 표시한것인데 검은색이 높은 확률을 의미하고 화살표들은 그 확률분포의 score를 나타낸다. score만 우리가 알아도 데이터를 그 score를 통해서 높은 확률로 이동시키면서 데이터를 생성할 수 있게 될 것이다.

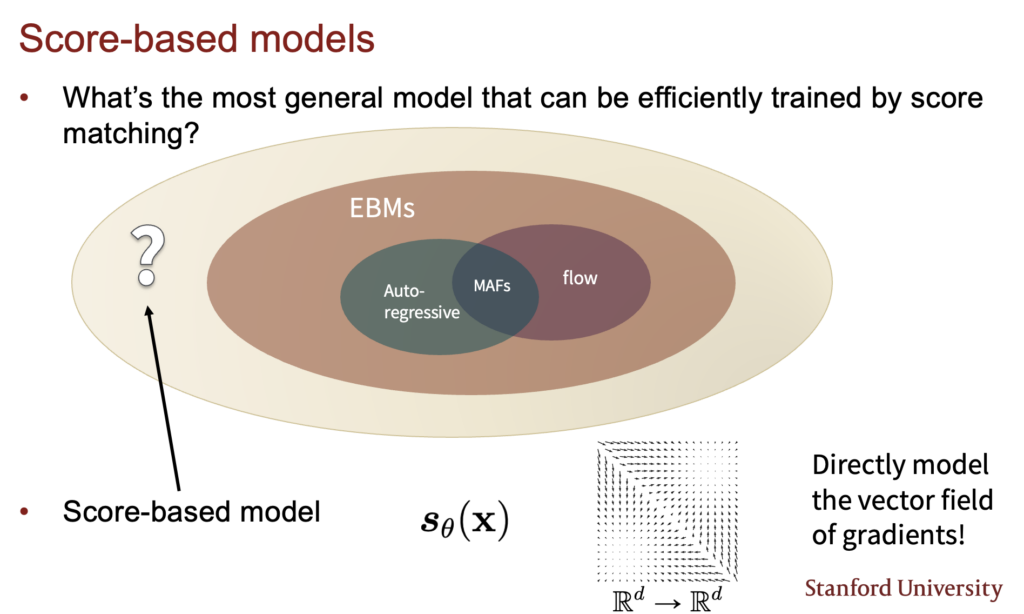
사실 이미 이전에 energy based model을 다루며 score matching을 설명하면서 이 방식을 다뤘는데 Score-based model이라는 개념은 좀 더 큰 개념이다. energy based model은 score-based model중에 일부분이고 energy based model이 아니여도 score based model을 만들 수 있는 방법은 많다.

이제 어떻게 score based model을 설계하고 학습시켜야할지 생각을 해보자. 우리가 가지고 있는건 training data의 분포이다. 정확하게는 아래 그림의 중간에 있는 training data의 i.i.d 샘플들이다. 이 sample들을 이용해 정확한 score function을 배우고 싶은것이다. 이러한 task를 score estimation이라고 하자.

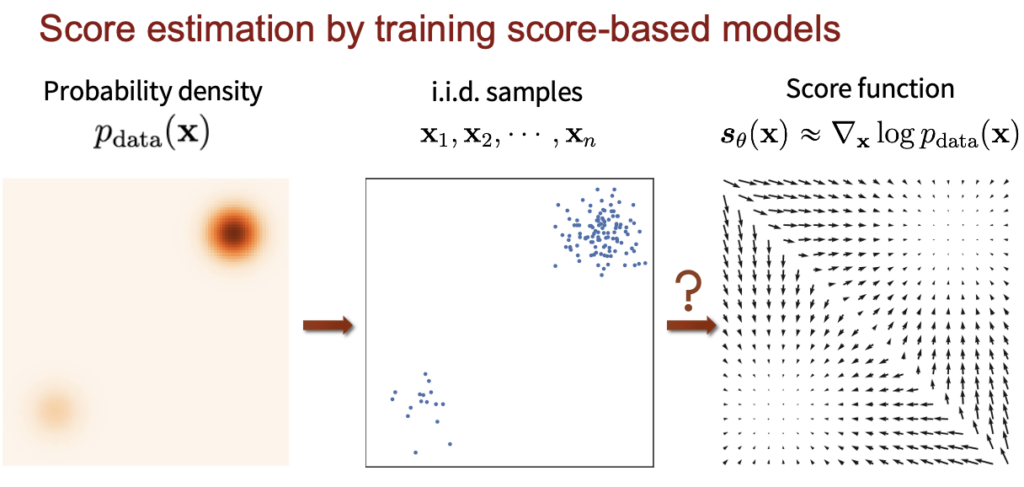
우리가 실제 데이터의 score (\( \nabla _x log p_{data}(x)\))를 알고있다고 하면 score (\( s_\theta\))모델과 차이를 계산해가면서 학습시키면 될것이다.

그래서 아래와 같이 objective를 설계할수 있다.

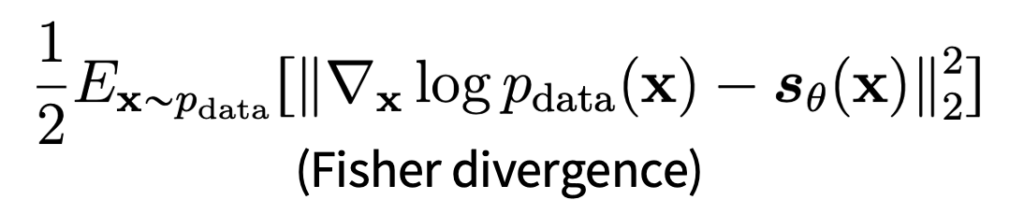
근데 사실 우리는 실제 데이터의 score (\( \nabla _x log p_{data}(x)\)) 를 모른다. (사실 이걸 알면 모델을 만들고 학습시킬 이유도 없다). 그래서 이전에 energy based model에서 위 식을 전개하고 변환해서 최종적으로 아래와 같은 score matching식을 얻어냈었다.

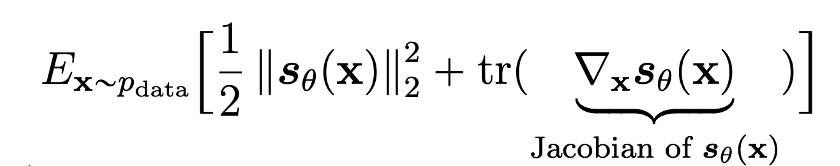
하지만 jacobian 계산이 들어가면서 연산이 너무 커져서 scalable하게 동작하지 않는다는 한계가 있었다.

이를 해결하고자 나오는 방법이 denoising score matching이고 본격적으로 현재 diffusion model 들이 사용하는 방식이 나온다. 아래 그림과 같이 기존 데이터에 가우시안 노이즈를 더해서 분포를 \(q_\sigma(\tilde{x})\)로 만든다. score도 기존 데이터가 아니라 노이즈가 더해진 데이터의 score를 예측한다. 그렇게 해서 식을 쭉 전개하면 아래의 식들이 쭉 전개된다.

이렇게 전개된 식의 마지막 결과가 아래와 같다.

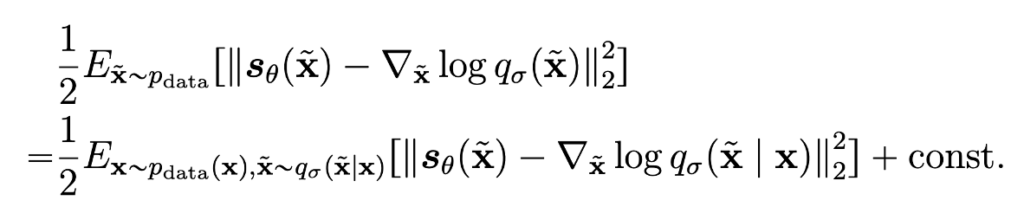
위식에서 \( \nabla _\tilde{x} log q_\sigma(\tilde{x}|x)\)는 굉장히 계산이 쉽다. 왜냐하면 \(q_\sigma(\tilde{x}|x)\)가 가우시안 분포이기 때문에 아래와 같이 계산이 가능해지기 때문이다.

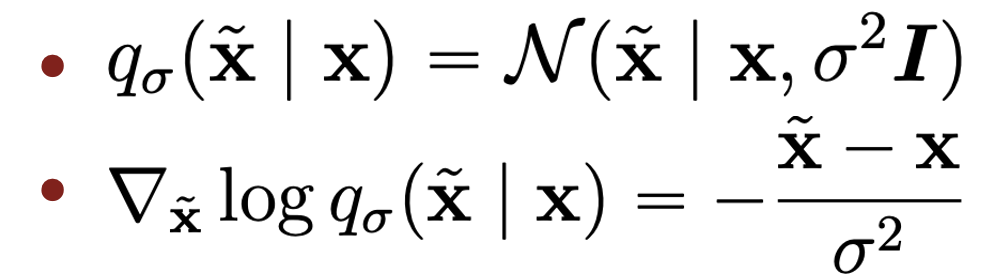
이제 \( \nabla _\tilde{x} log q_\sigma(\tilde{x}|x)\)의 값을 위의 loss식에 넣고 \( s_\theta \)를 학습시키기만 하면 score를 아주 쉽게 학습할 수 있게 되는것이다. 하지만 여기서 단점을 꼽으라면 우리는 데이터셋에서 clean한 이미지의 분포를 학습하는것이 아니라 noisy한 이미지의 분포를 학습하게 되는것이라는 문제가 있다. 그래서 \( \sigma \)값을 매우 작게 설정해서 노이즈를 엄청 작게 더해줘서 학습을 하게 된다.

최종적으로 denoising score matching 학습을 하는 방법은 아래와 같다. training dataset에서 sample을 뽑고, 가우시안 노이즈를 더하고, score estimation을 하도록 네트워크를 학습시킨다 (네트워크는 보통 Unet 구조)

사실 score matching식을 다시 봐보면 아래와 같이 단순히 \( s_\theta(\tilde{x}) \)는 원본 이미지 x에 더해진 노이즈를 예측하는 네트워크가 된다. loss식만 봐도 수식적으로 단순히 denoising을 학습하는건데도 이것이 score estimation이 된다. 즉, score estimation은 optimal denoising과 같다는 것이다.

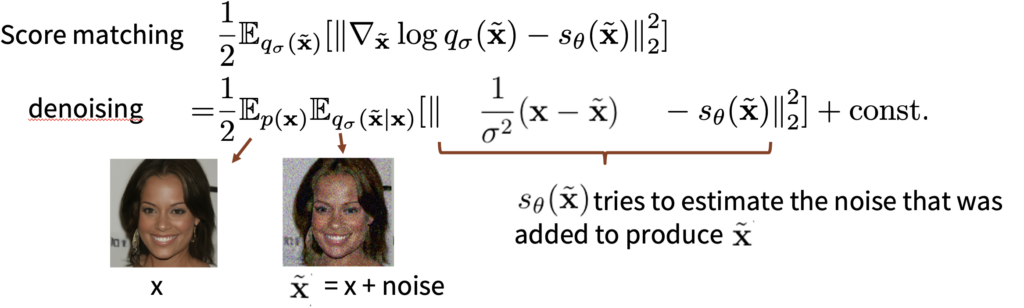
또 다른 방법으로는 sliced score matching이라는 방법이 있는데 요약하면 기존의 score matching 방법이 high dimension으로 가면 연산량이 너무 많아져서 scalable하지 않은건데 이를 아래 그림처럼 특정 벡터에 project해서 output 차원을 강제로 낮추면 데이터 dimension이 높아져도 계속 낮은 차원으로 최종 output을 얻을 수 있어서 scalable하게 연산을 할 수 있다는 것이다ㅏ.

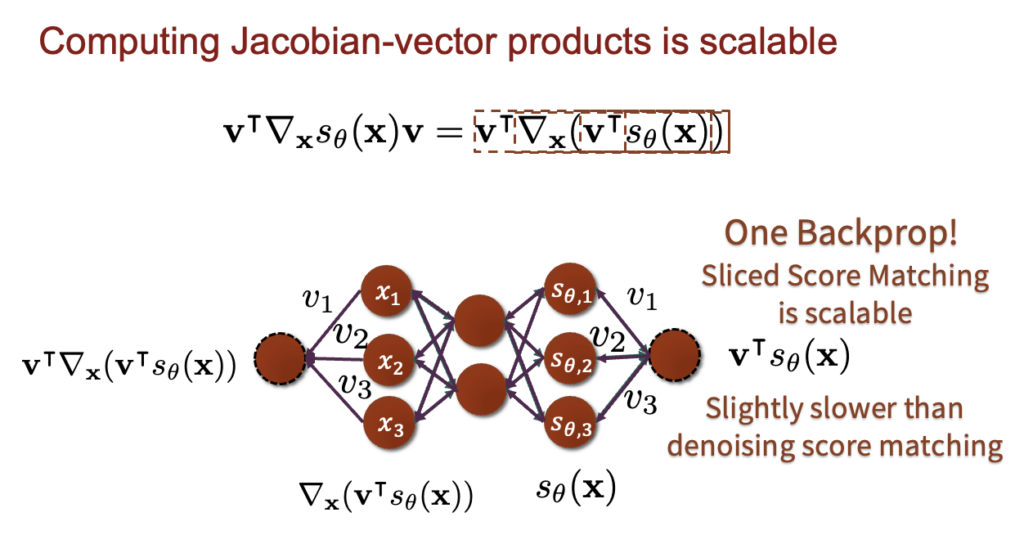
그래도 위의 denoising score matching 방식이 보편적으로 diffusion model에서 사용되는 방식이고 sliced score matching 방식은 많이 사용되지는 않는 방식인것 같다.

이제 이렇게 학습시킨 score estimation 네트워크를 가지고 어떻게 sample을 생성할 수 있을지 봐보자. 아래 그림은 sampling 방법을 시각화 한것이다. score가 마치 전기장처럼 펼쳐져 있고 random한 point에서 시작해서 score를 따라 데이터를 변환해가면 결국 높은 probability가 되는 데이터가 된다. 이때 local하게 빠지는것을 막기 위해 노이즈를 더해가면서 변환한다. 이를 Langevin MCMC 방법이라고 한다.

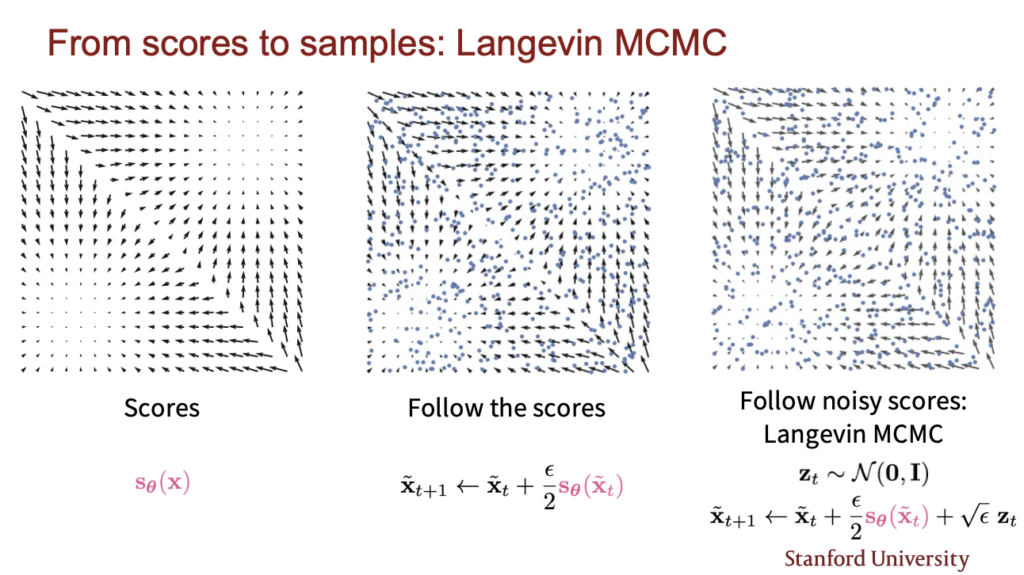
여기서 더해주는 \( \epsilon \)의 값을 줄이고 횟수를 늘리면 늘릴수록 실제 데이터와 더 가까워지고 반대로 \( \epsilon \) 값을 늘리고 횟수를 줄이면 approximation된 결과를 얻지만 실제로 거의 무시할만한 에러라고 한다.

근데 아직 해결해야되는 문제들이 남아있다. 위의 방식을 그대로 적용하면 아래와 같이 제대로 생성이 안된다.

해결해야되는 문제는 크게 3가지 정도로 구분되어있는데 다음 lecture에서 자세히 다루고 여기서는 간단히만 이야기하면

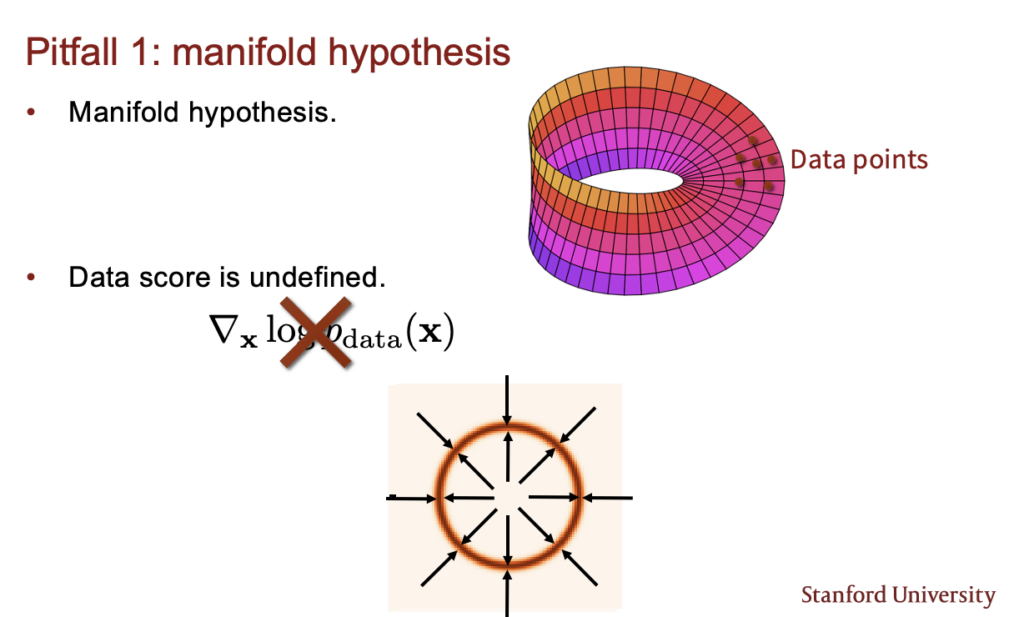
1. 첫번째는 manifold hypothesis 문제이다. 이는 실제 데이터가 실제 차원보다 저차원 공간에 존재해서 score vector가 정의될 수 없는 경우가 생기는 것이다.

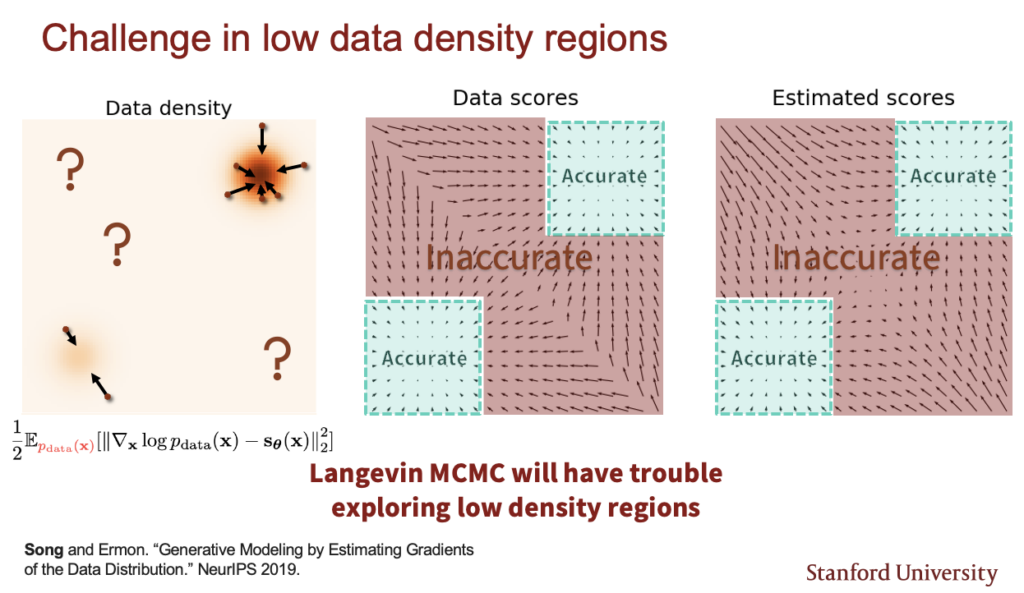
2. 두번째는 low data density region문제이다. 실제 데이터의 density가 낮은 지역에서는 score가 부정확할수 있다는 것이다. score는 기울기를 측정하는것이기 때문에, 어차피 데이터가 없는 지역들에서는 어디로 가야할지 기울기가 불명확해진다.

3. 마지막으로 Langevin dynamic의 slow mixing 문제이다. 여기서 mixing은 서로 다른 분포를 지닌 다른 data들이 섞여있는 경우이다. 둘이 특정 비율로 섞여있지만 이의 score 예측을 할때는 그 비율을 알수가 없다. 아래 식을 보면 서로 다른 두 데이터 분포가 \( \pi \) 비율로 섞여있는데 이에 대한 score를 계산할때는 \( \pi \)가 없어진다. 따라서 이에 비율에 대한 score estimation을 직접 학습을 못하기 때문에 오래 걸린다는 것이다.

위의 문제들을 모두 해결하면 아래와 같이 매우 훌륭한 퀄리티의 데이터를 생성할 수 있게 된다. 현재는 이 방식이 가장 보편적으로 사용되는 diffusion 방식이다.