[논문 리뷰] Image Restoration with Mean-Reverting Stochastic Differential Equations (IR-SDE) (2023 ICML)

SDE를 이용한 image restoration 방법을 제안한 논문이다.

git 주소 : https://github.com/Algolzw/image-restoration-sde

Introduction

기본적으로 SDE는 아래와 같은 방식으로 원래의 이미지에서 노이즈로 변환하는 Forward 식을 만들고 반대로 노이즈에서 이미지로 변환해주는 Reverse 식을 만들어 네트워크가 score 값을 예측하도록 학습시킨다. 이렇게 학습된 네트워크를 이용해 노이즈로부터 이미지를 생성한다.

Restoration task는 기본적으로 완전히 새로운 이미지를 생성하는 것이 아니라 이미지의 degradation을 복원하고 quality를 높이는것이 목적이다. 따라서 이 논문에서는 위의 SDE diffusion 방식을 이용해서 image restoration에 맞게 식을 만들어 아래와 같이 제안한다.

Method

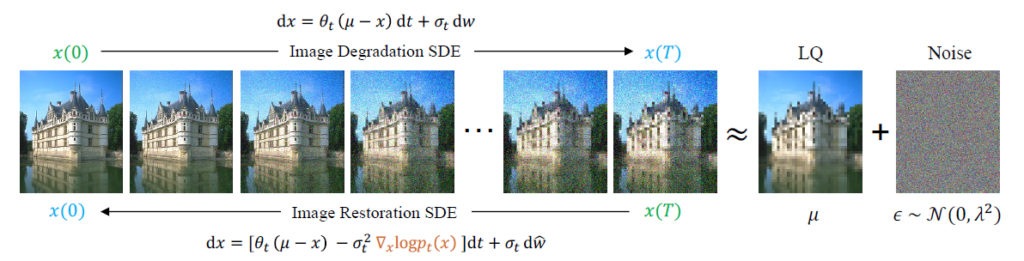
제안된 식에서 \( \mu \)는 degradation이 있는 LQ(Low Quality) 이미지이고 x(0)는 HQ(High Quality) 이미지이다. 즉, LQ와 HQ 이미지 pair가 존재하기만 하면 degradation 종류(noise, blur, rain 등)에 관계없이 학습을 시킬 수 있다. 실제로 많은 restoration task에 적용해 실험을 했고 결과가 상당히 좋았다. \( \theta \)와 \( \sigma \)는 time-dependent 변수고 노이즈가 더해지는 속도를 조절하는 역할을 한다. constant로 정하면 시간마다 똑같은 노이즈 양이 추가되고 linear나 cosine으로 세팅하면 시간에 따라 노이즈가 추가되는 양이 점점 증가되는식으로 작동하게 된다. 이 논문에서는 ablation 실험을 통해 cosine으로 노이즈를 추가했을 때 전체적으로 성능이 가장 좋았다고 한다.

Forward

\( \theta \)와 \( \sigma \)의 관계는 아래와 같이 정하고 식 전개를 시작한다.

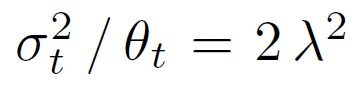
위의 방법으로 만들어진 noisy 이미지를 이용해 denoising 과정을 학습하는 과정은 일반적인 score-based model을 학습시키는 방법과 동일하다. 먼저 forward식을 풀어서 t시점의 noisy 이미지를 얻는다. (식의 전개과정이나 증명은 너무 길기도 하고 제대로 이해하지 못해서 생략… 궁금하신 분들은 논문을 찾아 appendix를 확인해보면 된다.)

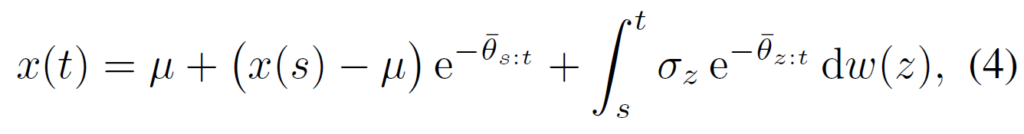
위의 forward식의 solution은 아래와 같이 표현할 수도 있다.

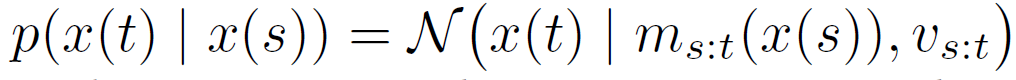
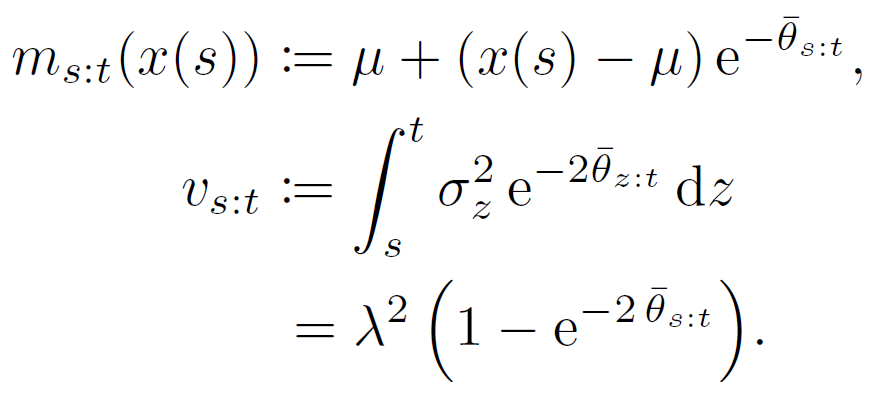
즉 t가 무한으로 가면 x(t)는 mean이 \( \mu \)이고 variance가 \( \lambda \)인 signal이 된다. 즉 LQ이미지에 특정한 level의 가우시안 노이즈가 더해져 있는 이미지가 되고 그러한 이미지로부터 HQ를 얻도록 Reverse process가 진행된다.

Reverse

이를 이용하면 Reverse process 학습에 필요한 ground truth score도 아래와 같이 구할 수 있다.

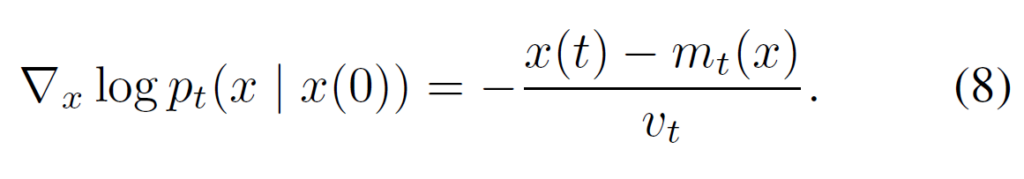
x(t) = m + \( \sqrt{v} \) \( \epsilon \) 이므로 위의 식에 넣으면 아래와 같이 최종적으로 ground truth score를 간단하게 구할 수 있다. (\( \epsilon \)은 가우시안 노이즈이다. )

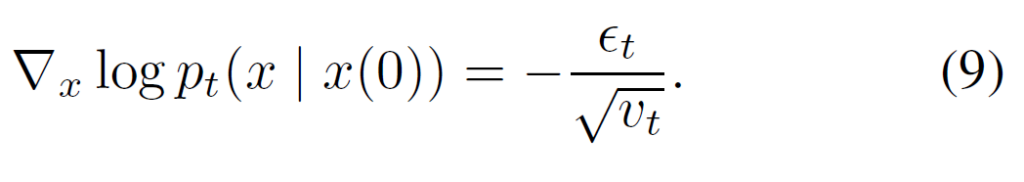
이제 일반적인 Diffusion 모델처럼 input으로 x, \( \mu \), t를 input으로 받아 score를 예측하는 U-net 구조의 network를 만들고 DDPM처럼 아래와 같은 Loss로 학습시키면 끝이다.

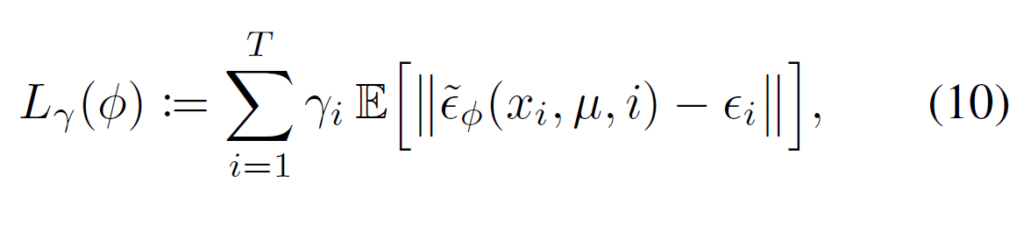
Maximum Likelihood object

위와 같은 loss로도 simple하게 학습을 할 수 있지만 논문에서는 위와 같은 loss를 썼을 때 복잡한 degradation에 대해서는 학습이 조금 unstable하다고 했다. 이는 특정 시간의 노이즈를 바로 예측하게 해서 생긴 문제라고 추측하면서 대신해서 사용할 Maximum Likelihood object를 제안하고 score를 직접 예측하는것이 아닌 1~T까지 의 이미지 변화 trajectory를 더 정확하게 예측하고자 했다.

이를 위해 먼저 reverse process의 solution을 아래와 같이 얻어냈다. (증명은 pass….)

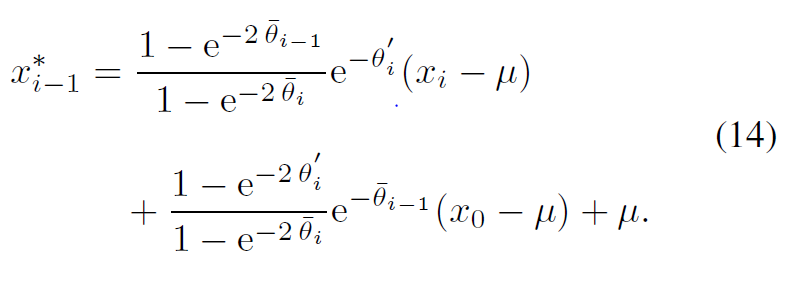
이를 이용해 아래와 같은 loss function을 새로 제안했다.

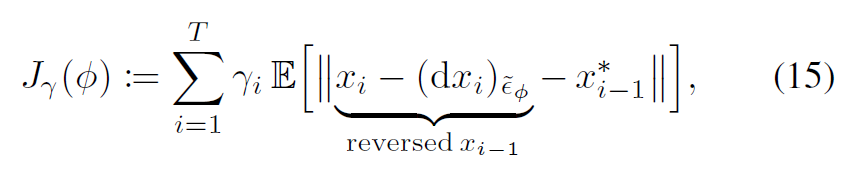
dx는 network를 이용해 예측한 noise여서 \( x_i \) – \( dx_i \)는 네트워크를 통해 예측된 reverse process가 된다. \( x^{*}_{i-1} \)는 ground turth가 되어 reverse process가 optimal인 ground truth를 잘 생성하도록 학습이 되는 것이다.

Experiments

다양한 실험에 대해 좋은 결과를 내는데 특히 restoration task에서 평가 지표로 많이 쓰이는 PSNR, SSIM 이런 수치들보다 실제 눈으로 봤을 때의 perception 관련 성능이 매우 좋아지는 것 같다.

아래의 table은 deblurring task에 대해서 다른 방법들과 성능 비교를 한 것인데 사실 PSNR만 놓고 보면 그렇게 좋은 수치는 아닌것처럼 보인다. CNN-Baseline은 diffusion에서 쓰인 네트워크를 diffusion 방식으로 학습시키지 않고 그냥 end-to-end로 input에 LQ output에 HQ가 나오도록 학습 시킨 것이라고 하는데 그런 단순한 방법이랑 비교해도 PSNR에서는 크게 차이가 난다는 느낌은 안든다. 하지만 실제 visual 결과는 다른 방법들보다 명확히 훨씬 좋은 것 같고 LPIPS나 FID 수치가 확실히 차이가 나게 좋아진 것을 알 수 있다.

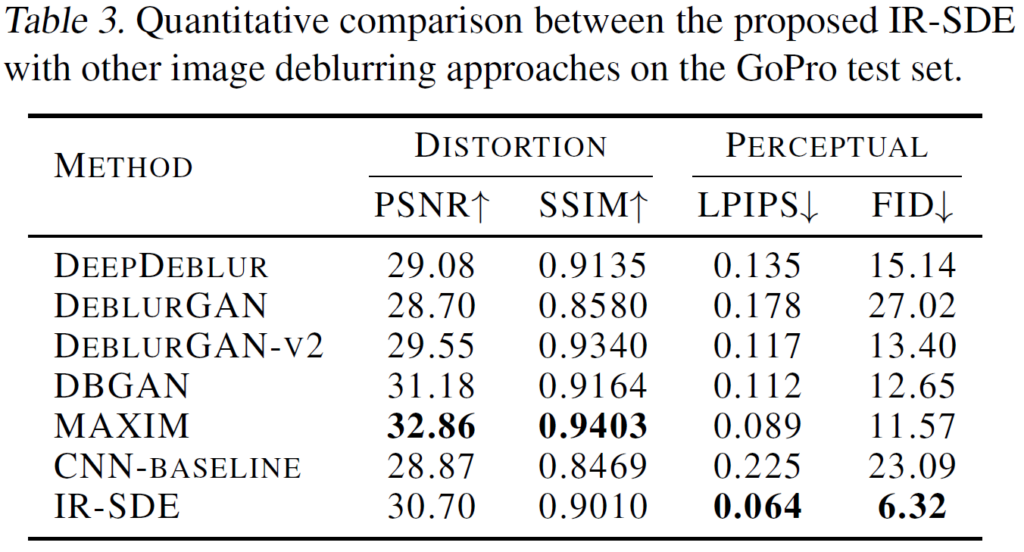
이에 대한 생각으로는 Diffusion process가 원래의 HQ를 복원하기 위해 pixel값만 단순히 가깝게 만든다기 보다는 특정 degradation을 점점 완화하는 느낌으로 진행되어 시각적으로 더 깔끔하게 복원된 결과를 얻을 수 있고 이는 ground truth인 HQ와 pixel값의 차이가 날 수 있기 때문이라고 생각된다.

아래는 복원 과정이다.

이 외에도 inpainting, dehazing등 다양한 restoration task에서 모두 좋은 결과를 보여준다.

Limitation 및 conclusion

이 논문에서 얘기하는 한계점의 포커스는 \( \theta \)와 \( \sigma \) 값 세팅에 있다. cosine 스케줄링이 성능이 가장 좋긴 했지만 cosine 스케줄링도 보면 아래와 같이 time step이 큰 부분에서 variance 값이 over-smooth 해진다. 즉 time-step이 큰 부분에서는 사실상 time step별로 이미지의 노이즈가 거의 차이가 안 나고 이것이 학습을 조금 어렵게 만든다고 얘기한다. 이를 해결하는것을 future work으로 남겨놓고 있다.

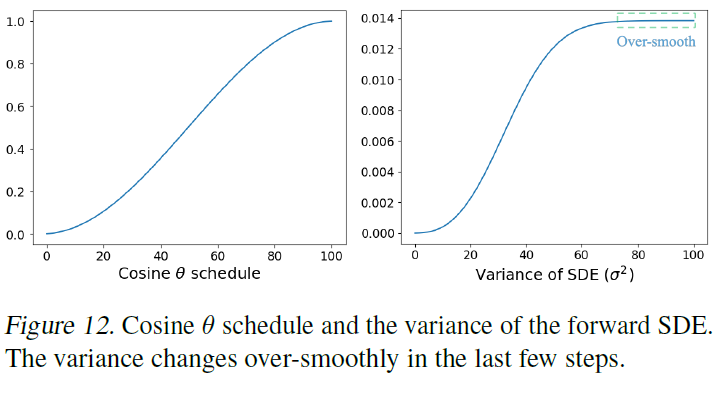
개인적으로 생각하는 가장 큰 limiation은 속도이다.다른 end-to-end 기법들은 이미지 한 장 처리하는데 보통 아무리 오래 걸려도 0.1초 미만으로 걸린다. 하지만 이 방법은 1K 이미지 한 장 처리하는데 거의 1분이 걸리는 것을 확인했다. 따라서 datsaet의 validation 시간도 굉장히 오래 걸리고 real-time으로 쓰는 건 불가능한 수준이었다. 이는 어쩔 수 없는 diffusion 방법의 한계점인것 같다. 이를 해결하는 것이 diffusion 방법을 restoration에서 쓰기 위해 가장 중요한 work일 것 같다.