[논문 리뷰] Fourmer: An Efficient Global Modeling Paradigm for Image Restoration(2023 ICML oral)

Introduction

 예전에 리뷰했던 Fast Fourier Convolution (2020 NIPS)와 비슷한 컨셉을 이미지 복원 분야에 적용한 논문이다. 

 Fourier Transform을 통해 이미지를 주파수 영역으로 보내주게 되면 픽셀 값 하나하나 이미지의 global 정보를 갖게 되는데 이를 이용해 1×1 convolution만을 이용해 적은 연산량과 parameter 수로 효율적인 연산을 가능하게 하는 방법이다.

 이 논문에선 Fourier Transofrm을 이미지 복원 분야에 적용하게 된 motivation에 대해서 아래 그림과 같이 제시한다.

 위의 그림을 보면 degraded 이미지와 clean 이미지를 각각 Fourier 영역으로 변환하고 amplitude끼리만 서로 바꿔주면 위의 (a),(b),(c) 같은 결과가 나온다. 보통 phase영역에 이미지의 특징이 더 많이 남아있고 amplitude에 degradation이 주로 존재해서 amplitude끼리 바꾸면 degradation이 전달되는 느낌이 강하다. 위의 그림에서도 (a)에서 hazy 성질이 amplitude를 바꾸면 원래 clean 이미지로 옮겨가고 (c)에서 low-light 성질도 amplitude끼리 바꾸면 그런 성질이 옮겨가는 등의 현상을 보인다.

 따라서 Fourier transform은 이미지 degradation에 대해 어느 정도 prior(사전 지식)를 가지고 있다고 주장하며 이게 fourier transform을 네트워크에 적용하게 된 motivaiton이 되었다고 한다. 

Method

arhcitecture

 이제 이 논문에서 제시하는 architecture 구조를 봐보자. overview figure는 아래와 같다. 

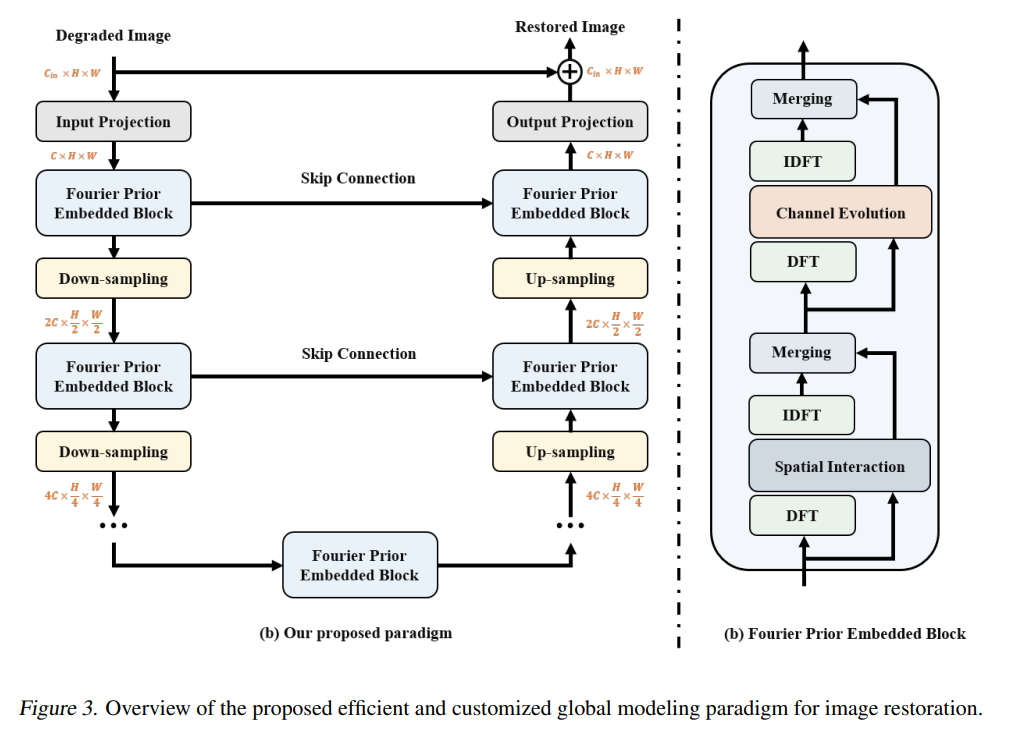
기본적으로 U-shape의 구조를 가지고 있고 input projection, output projection은 단순 채널 수 조절 역할을 하고 down-sampling, up-smapling은 3×3 convolution을 stride 2로 적용해서 feature map 사이즈 조절 및 채널 수 조절 역할을 한다. 여기까진 그냥 기존 U-net 구조인데 중간에 그냥 convolution block들이 들어가는 대신 FPE 라는 Fourier Prior Embedded Block을  넣어준다. FPE Block은 오른쪽 figure와 같은데 Spatial Interaction 부분과 Channel Evolution 부분으로 나뉜다. 이에 대한 자세한 figure는 아래 그림에 나와있다. 

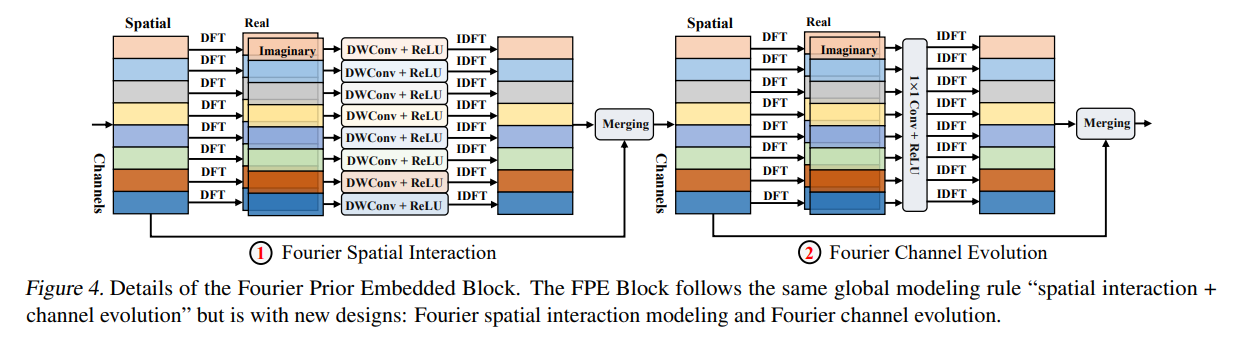
 먼저 Spatial Interaction 부분을 보면 먼저 feature map을 채널별로 DFT 변환을 한다. DFT 변환을 하면 실수(real) 부분 허수(Imaginary) 부분으로 나뉘게 되고 각각 depthwise-convolution, relu activation을 적용한다. 이후 Inverse DFT를 적용해서 다시 spatial domain으로 옮겨주고 이전 featuremap과 merging 해주는데 여기서 merging은 concatenation을 한다고 한다. 식으로 표현하면 아래와 같다. 

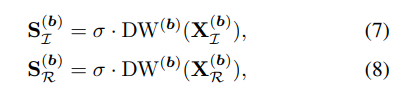
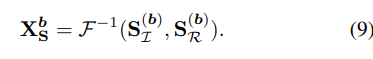
 다음은 Channel Evolution이다 마찬가지로 feature map을 DFT변환을 해주고 이후에 Real 부분과 Imaginary 부분을 각각 1×1 convolution으로 채널간의 정보를 섞어준다. 이전에는 Depthwise convolution이어서 각 채널간 정보가 섞이지 않는데 이 부분에서 channel간 정보가 섞인다. 그래도 phase와 real 부분은 분리해서 phase와 real 채널간의 정보가 섞이지는 않는다. 이후 마찬가지로 merging해서 내보내주면 하나의 FPE Block 연산이 완료된다. 이 부분도 식으로 표현하면 아래와 같다.

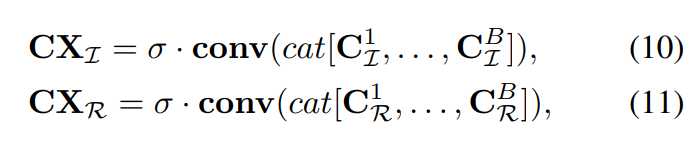
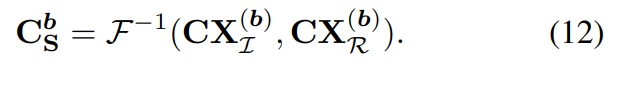
loss

다음은 loss function이다. 기본적으로 spatial domain에서 L1 loss를 적용하고 frequency domain에서도 L1 loss를 적용한다. frequency domain에서 L1 loss를 적용할때는 amplitude와 phase 영역을 각각 나눠서 L1- loss를 적용한다. 식으로 표현하면 아래와 같다.

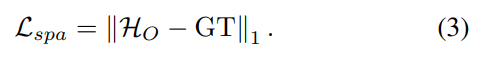
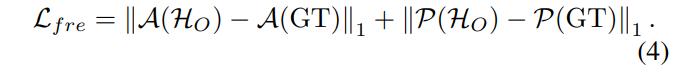
Experiments

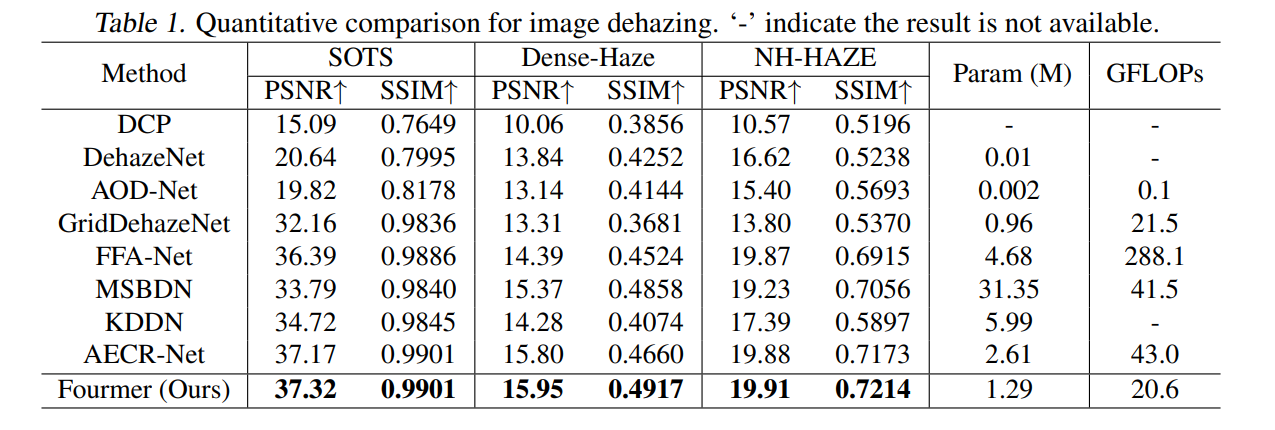
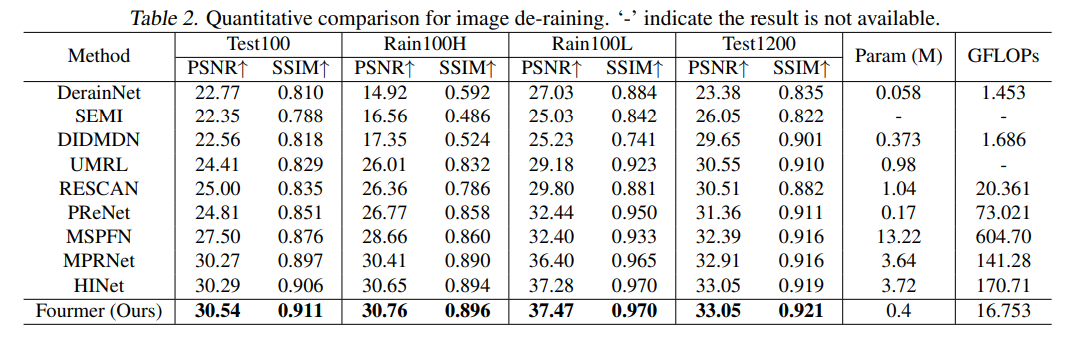
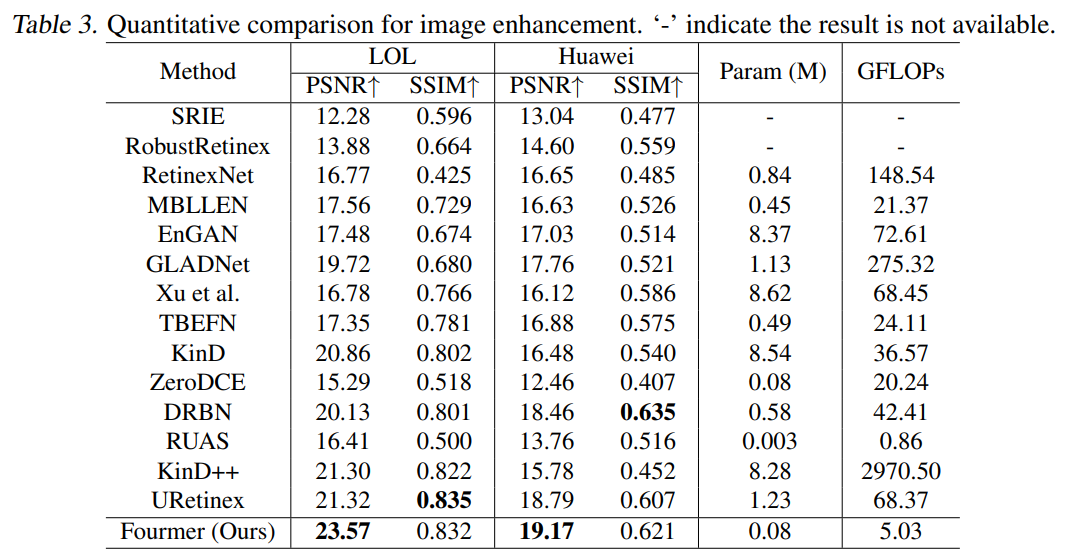
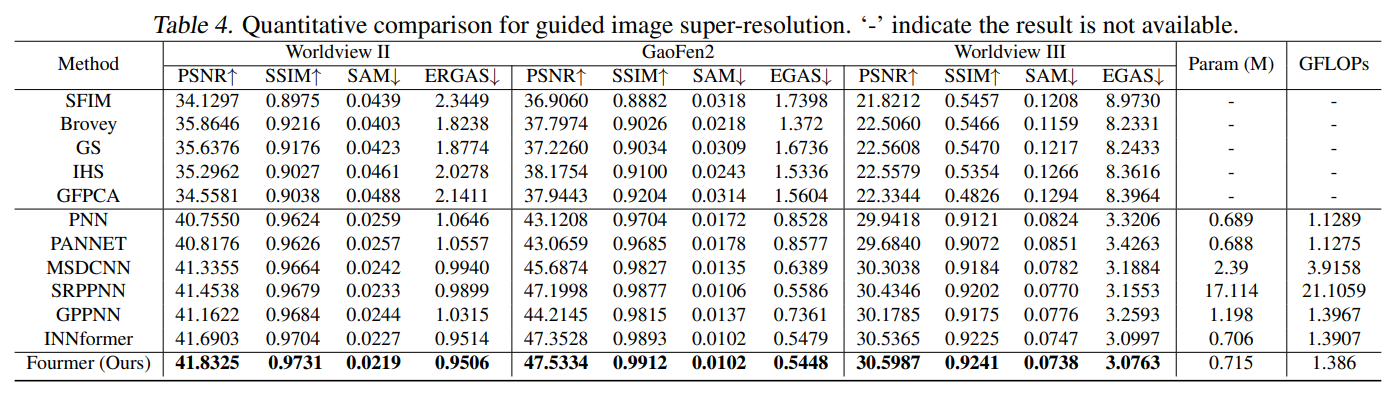
이를 각각 image dehazing, de-raining, image enhancement, image super-resolution에서 실험하고 결과를 측정했다. 기본적으로 depthwise convolution 및 1×1 convolution위주로 구성되어 있어서 파라미터와 연산량이 작다. 그럼에도 불구하고 좋은 성능을 낸다. 

Conclusion

 Fourier transform을 이용해 적은 연산으로도 좋은 성능을 내는 image resotration model.