[Generative Artificial Intelligence] Energy Based Models – 2

Stanford CS236 Deep Generative Models 수업의 자료를 기반으로 생성모델의 기본 개념들을 정리해보고자 한다. (참고 https://deepgenerativemodels.github.io/syllabus.html)

이전 포스팅에서 energy based model을 학습시키기 위한 방법인 Contrastive Divergence를 설명하고, 학습을 위해서 sampling을 해야하기 때문에 sampling을 하는 방법까지 소개했다. 아래에 내용이 정리되어 있다.

위 슬라이드에서 나와있듯이 dimensionality가 커지면 sampling의 convergence 속도도 매우 느려지고, sampling하는데 걸리는 시간도 큰데 학습하는 매 iteration마다 sampling해야하기 때문에 학습하는데 시간이 너무 오래 걸릴 수밖에 없다. 그래서 이번 lecture에서 목표는 sampling없이 energy based model을 학습시키는 것이고 아래의 3가지 방법 1. Score matching, 2. Noise Contrastive Estimation, 3. Adversarial Training 에 대해 소개한다.

첫번째로 나오는 내용은 Score matching이다. \( p_{data} \)와 EBM모델 \( (p_\theta) \)의 Fisher divergence를 최소화하도록 학습하는 것이다. Fisher divergence를 계산하는 방법은 아래와 같다.

위 식에 EBM모델 \( (p_\theta) \)을 적용해보면 \( \nabla _x log p_\theta(x)\)가 되고 이 식이 바로 score function\((s_\theta) \)이니까 \( p_{data} \)와 EBM모델 \((p_\theta) \)의 score matching 식이 아래와 같이 된다.

위 식을 전개하는 과정은 아래에 나와있다.

위의 마지막 식으로 결국 score matching loss를 측정할 수 있게 된다.

위에서 모든 data의 기댓값을 한번에 측정할순 없으니 Stochastic Gradeint Descent (SGD) 방식으로 sample을 batch단위로 가져와서 loss를 측정해 업데이트하면 된다. 위 식에서 \( \nabla _x log p_\theta(x)\)는 \( \nabla _x f_\theta(x)\)이기 때문에 최종적으로 아래와 같은 식으로 바꿔 표현할수도 있다. 이제 training 할때 sampling을 하지 않고도 아래 loss만을 측정해서 EBM모델을 학습시킬 수 있게 되었다.

그런데 위에 슬라이드에 나와있드듯이 최종식에서 Hessian matrix의 trace를 측정해야되는 부분이 있는데 모델이 커지면 이 값을 계산하는게 연산량이 굉장히 커진다는 한계가 있다.

두번째로 소개되는 방법은 Noise contrastive estimation 이다. 이름 그대로 noise와 constrastive하게 비교를 해서 학습을 하겠다는것이고 이때 discriminator를 사용한다. Discriminator는 데이터 x가 noise인지, 실제 data인지 구분하도록 학습이 된다. 그러면 학습방법은 아래의 식을 maximize하는것이다.

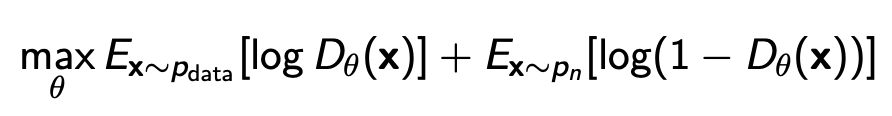
GAN에서 다뤘듯이 이때 optimal한 Discriminator는 아래와 같다.

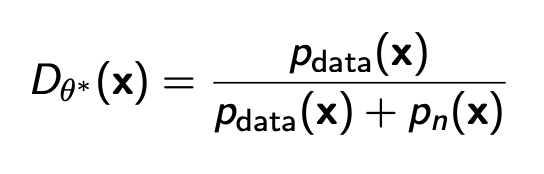
\( p_{data} \)는 실제 data의 확률이 되고 \( p_n \)은 noise의 확률이다. 그러면 이 discriminator의 파라미터를 \( \theta \)라고 하고 이를 optimize해서 \( \theta*\)을 얻으면 아래와 같이 얻어진다.

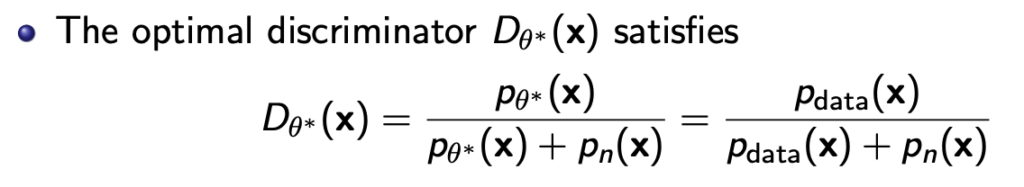
즉 discriminator를 학습시키는것이 implicit하게 \( p_\theta* \approx p_{data} \)가 되도록 만드는것임을 나타낸다.

그리고 NCE 방법을 쓸때는 Z도 파라미터화 해서 trainable하게 만들어 학습시킨다.

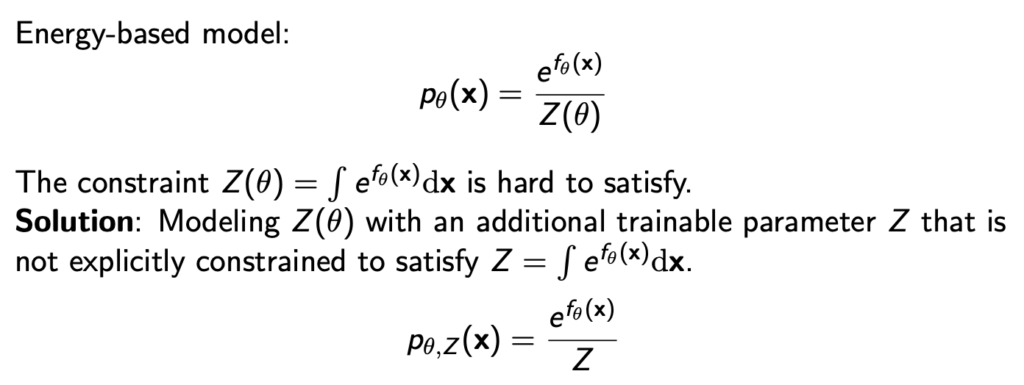
위의 \( p_{\theta, Z} \)를 이제 discriminator에 대입해서 이를 학습시키기 위한 loss식을 아래와 같이 정리할 수 있다.

최종 NCE 방법으로 학습시키는 과정은 아래와 같다. trianing data에서 sample을 뽑고, 노이즈 분포에서도 sample을 뽑고 이 sample들로 최종 NCE loss를 계산하고 SGD 방식으로 \( \theta와 Z \)를 업데이트 해나간다. 그러면 우리가 원하는 energy based model이 implicit하게 학습이 된다.

위의 NCE방법에서는 noise의 분포가 실제 데이터의 분포와 매우 다르면 구분하기가 너무 쉬워져서 복잡한 데이터에 대해서는 학습이 잘 안된다는 단점이 있다고 한다. 그래서 노이즈의 분포를 data와 유사해지도록 같이 학습시키는 Flow contrastive estimation등의 방법도 있다고 한다.

마지막 3번째가 adversarial training인데 별건 없고 그냥 variational 분포 \( q_\phi \)를 하나 만들어서 energy based model의 log-likelihood의 upper bound를 만든다음 이전의 latent variable model 학습시킬 때처럼 upper-bound를 minimize해서 원래 값과 근사하고 그 근사된 값을 maximize하는 방식대로 학습시키는 것이다.