Stanford CS236 Deep Generative Models 수업의 자료를 기반으로 생성모델의 기본 개념들을 정리해보고자 한다. (참고 https://deepgenerativemodels.github.io/syllabus.html)
이전의 Autogressive Model 같은 경우에는 likelihood 계산도 직관적이라 쉽고 학습하기도 쉽지만 sequential하게 생성하기 때문에 오래걸리기도 하고 생성하려고 하는 데이터의 특징을 전혀 학습할 수 없다는 단점이 있다. (단순히 확률대로 계속 sampling되는것일 뿐)
하지만 실제로 데이터들에는 특징이 존재한다. 얼굴이라고 하면 성별, 눈 색깔, 머리 색깔 등등 다양한 특징이 존재한다. 이전의 autoregressive model은 이러한 특징을 담아 생성할수가 없는데 latent variable model은 이러한 특징을 z라는 변수로 explicit하게 만들어보고자 하는 motivation에서 출발한다. 하지만 문제는 이러한 특징들을 학습하려면 데이터셋에 이미지, 특징들이 같이 annotation이 되어있으면 편한데 사실 특징이라는것들이 정하기 나름이고 명확한 기준이 없어 annotation을 만들기는 어렵고 아래 그림처럼 매우 복잡해질수도 있다. 그래서 그냥 neural network에 맡겨버리자는 것이 latent variable model의 시작이 된다.
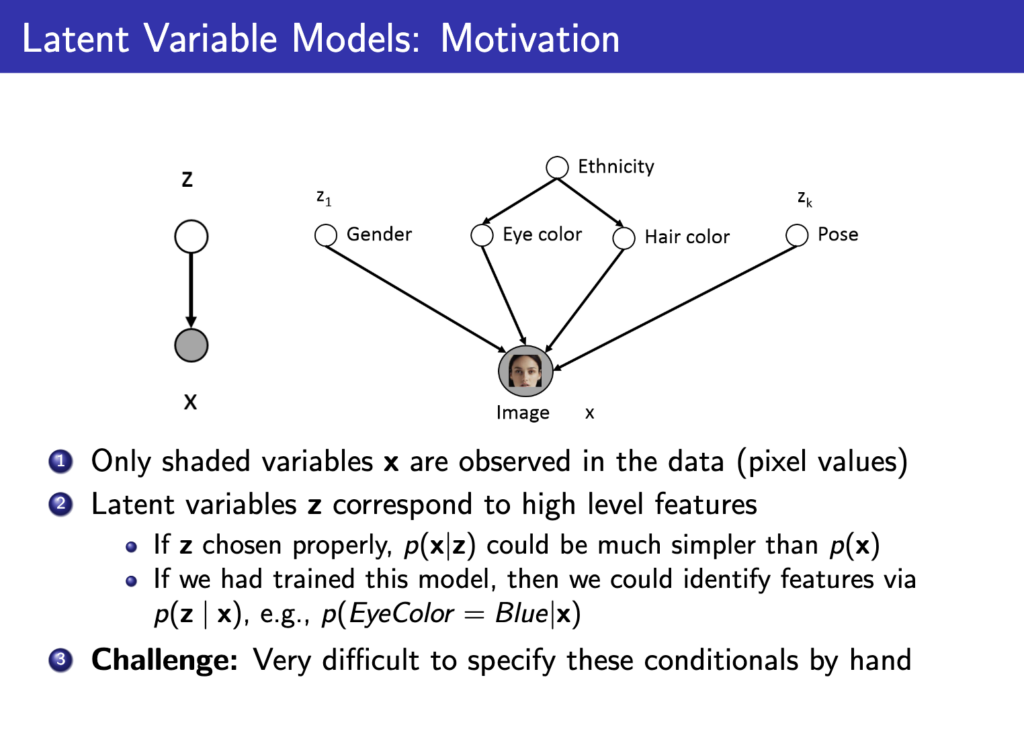
위 그림에서 ethnicity, gender 등등을 직접 만들지 않고 그냥 random 변수로 initialize한다음에 neural network에 입력으로 넣어서 아래 그림처럼 사용하게 된다. 이것이 Deep Latent Variable Model이다.
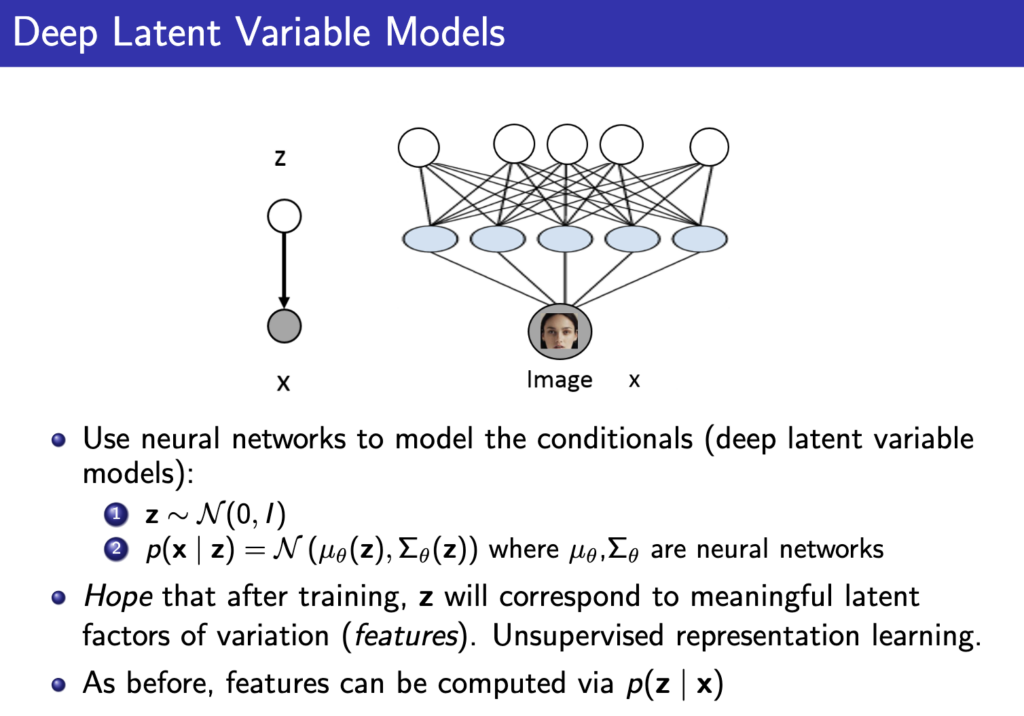
위의 그림을 보면 z로부터 p(x|z)의 분포를 만들고자 하는거고 neural network에 z를 넣어 mean 과 covariance matrix를 얻어내서 이를 이용해 가우시안 분포로 p(x|z)를 모델링 할 수 있다.
이를 쉽게 이해하기 위해 mixture of Gaussian으로 예시를 들어보자. K개의 서로 다른 z가 있다고 하자. 이때 p(x|z)는 가우시안 분포이고 z에 따라 각각 특정한 mean and covariance matrix를 가지는 확률분포가 된다(z는 class 같은 역할을 하게 된다.)
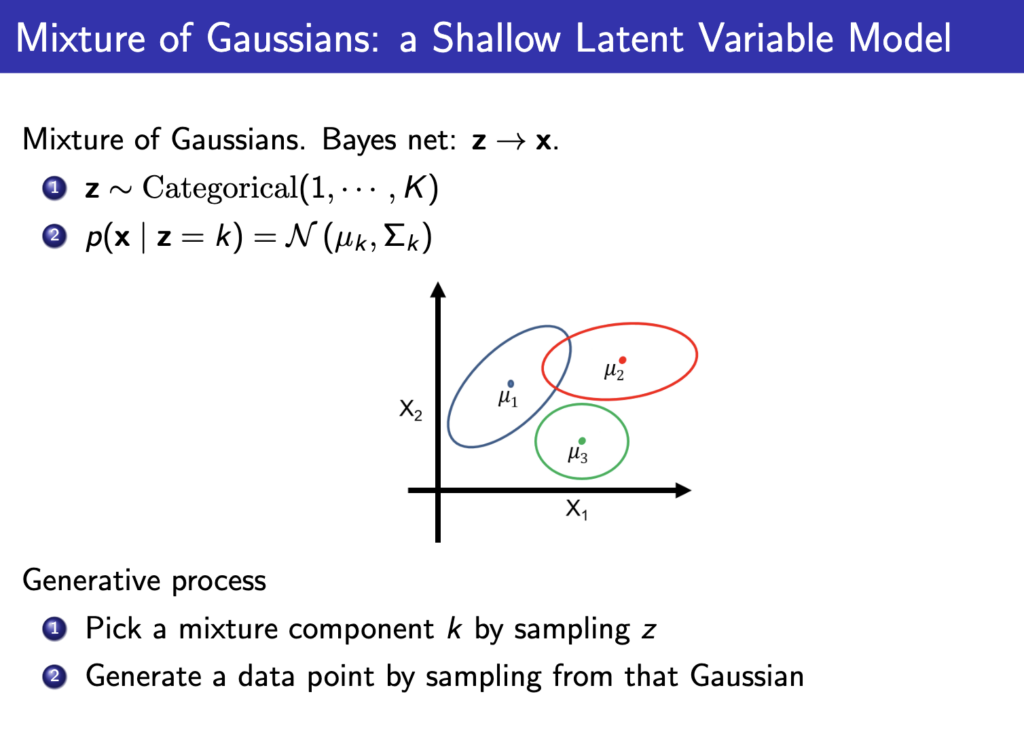
그러고 아래와 같이 실제 데이터들에 대해 적용해보면 K가 1이면 아래 이미지에서 가운데처럼 가우시안 하나로 분포를 표현하게 되지만 K가 2면 2개의 확률분포로 데이터를 더 잘 표현할 수 있게된다.

아래처럼 1~9까지 숫자를 확률분포로 표현하고자 할때 K값 (클러스터 갯수)를 크게 잡으면 아래 처럼 같은 숫자여도 조금씩 다른 cluster로 구분할 수 있다( ex, 기울어진 1, 똑바로 서있는 1). 즉, 숨어있는 feature를 z로 구분할 수 있게 된다는 이야기이다.

그리고 이렇게 z를 이용하면 p(x|z)는 단순한 가우시안 분포여도 p(x)는 아래와 같이 복잡한 분포를 표현할 수 있게 된다.
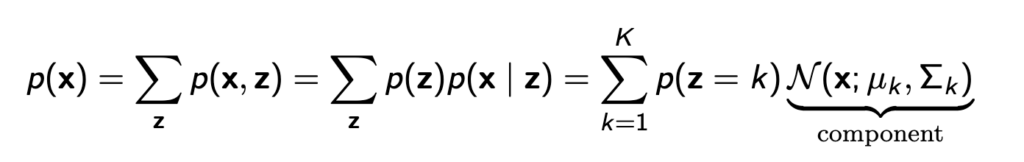
따라서 간단한 모델들로만 만들어도 복잡한 분포를 표현할 수 있다는것이 장점이고, 위의 예시처럼 자연스럽게 z가 구분돼서 unsupervised learning이 가능하다는 장점이 있다. 하지만 p(x)에 대해 maximum likelihood를 구해서 쉽게 학습할수 있는 autoregressive 모델에 비해 z가 들어가면서 학습이 어려워진다. 예시를 들기 위해 아래 그림처럼 일부 값이 없는 MNIST이미지들을 생각해보자.

여기서 가려진 부분이 z라고 하고 관측된 부분을 x라고 하자. 이제 p(x)를 구하기 위해서 아래와 같이 x에 대해 marginalize해서 \( p_\theta(x) \)에 대해 maximum likelihood를 구하고자 한다.
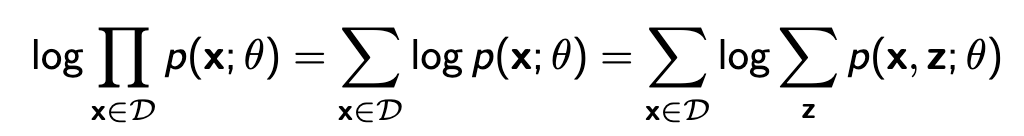
위 식을 계산하기 위해 모든 z에 대해서 \( p_\theta(x,z) \)를 구해야 하는데 z가 binary값으로 30 dimension만 돼도 (\( \{0,1\}^{30} \)) \( 2^{30} \)개의 term이 생긴다. 보통 이런 문제를 해결하기 위해 Monte Carlo 방식을 적용하게 된다. z값을 sampling 해서 k개만 뽑아 계산하는것이다.

하지만 위 슬라이드에 나와있듯이 이론적으로는 가능하지만 z가 너무 많은 가짓수가 있는 상황에서 잘 작동하는 방법은 아니다. 대부분의 z에서 \( p_\theta(x,z) \)가 굉장히 낮을 것이기 때문이다. (위 가려진 MNIST이미지를 생각해보면 observed된 픽셀값들과 z가 잘 매칭이 돼서 전체적으로 숫자처럼 보이는 z의 경우의 수가 전체 경우에 비해 얼마나 될까? 거의 대부분 경우 z를 랜덤으로 설정하면 제대로 된 숫자처럼 안보일 것이다). 따라서 단순 Monte Carlo 방식보다 조금 더 개선된 방식으로 z를 sampling해서 사용하고자 하는것이 아래 슬라이드이다.

요약하면 q(z)라는 분포를 하나 새로 만들거고 q(z)로부터 z를 sampling해서 \( p_\theta(x) \)의 maximum likelihood를 계산하기 위한 Monte Carlo 방식에 적용할 것이라는 얘기이다. 이게 Importance Sampling 방법이다. 이게 잘 작동하려면 q(z)가 그럴듯한 z에 대해서 높은 확률을 얻도록 되어야될것이다. q(z)가 잘 설정되면 그로부터 sampling된 z는 중요하고 그럴듯한 z가 많이 생길거고 \( p_\theta(x,z) \)또한 충분히 높은값이 많이 나올것이고 \( p_\theta(x) \)도 더 정확하게 구할 수 있을 것이다. 그렇다면 q(z)는 어떻게 얻는가? 이를 위해 다시 \( p_\theta(x) \)를 구하는 과정부터 살펴보자.
우리가 최종적으로 구하고 싶은것은 아래와 같은 \( p_\theta(x) \)의 log likelihood이다. 바로 위 슬라이드에서 첫번째 식에 log를 씌워 구하면 아래와 같은 식으로 바뀌고 log함수의 성질에 의해 아래와 같이 lower bound가 생긴다.

위의 슬라이드에서 f(z)가 \( p_\theta(x,z) / q(z) \) 가 되는거고 이를 대입해서 식을 표현하면 아래와 같이 ELBO(Evidence Lower Bound)라고 하는 lower bound가 생긴다.
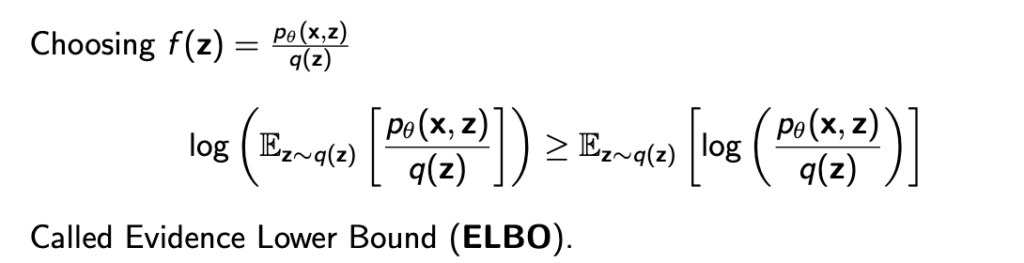
따라서 q가 무슨 분포던간에 \( log p_\theta(x) \)는 아래와 같이 ELBO를 갖는다.
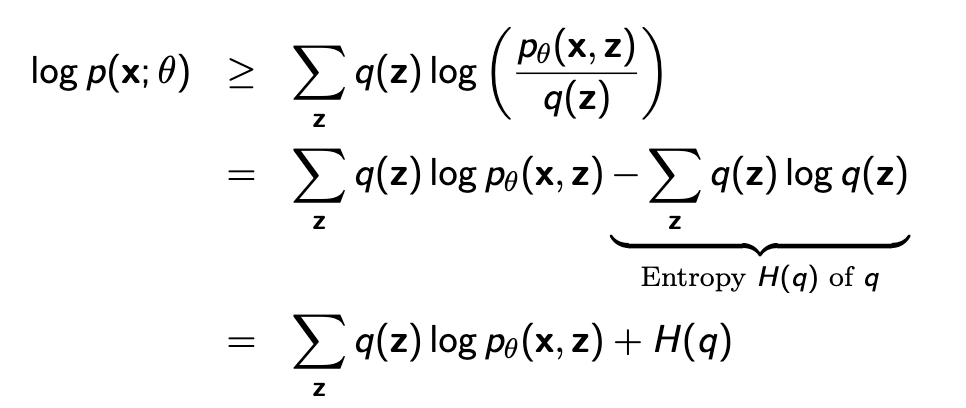
이때 q(z)가 \( p_\theta(z|x) \)와 같을때 위의 식이 equality가 된다.
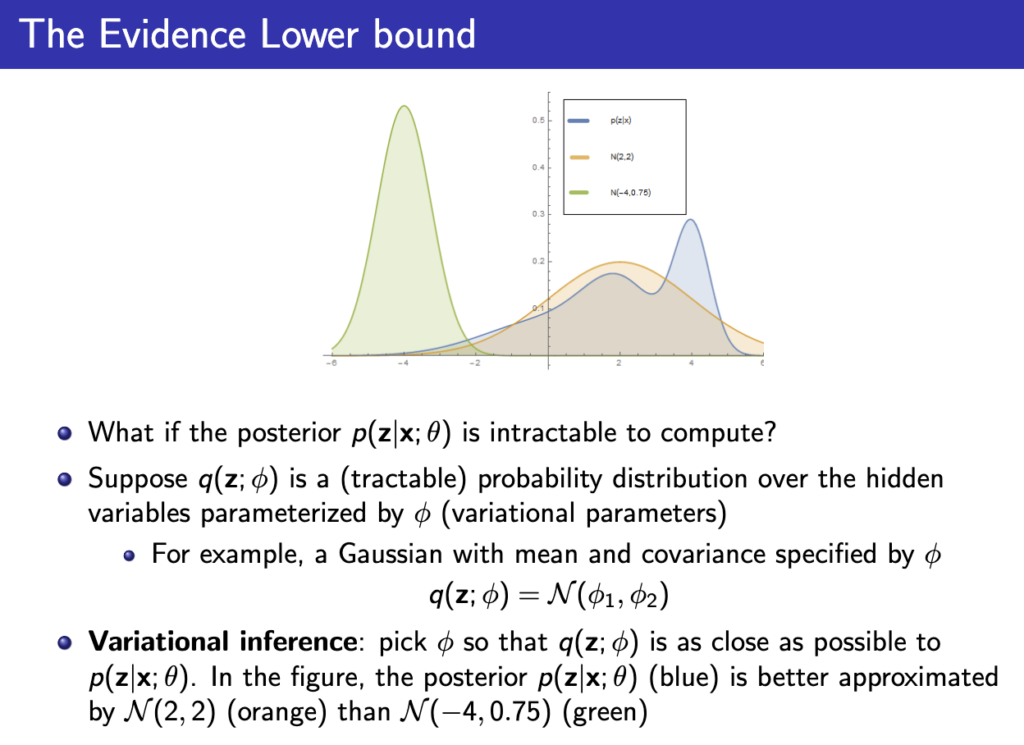
우리가 구하고 싶은값이 \( log p_\theta(x) \) 이니까 q(z)를 그러면 \( p_\theta(z|x) \) 와 같게 설정하면 q를 이용해 \( log p_\theta(x) \) 를 구할 수 있게 되는것이다. 근데 그러면 또 \( p_\theta(z|x) \)는 어떻게 알아야하는가… 대부분 \( p_\theta(z|x) \)는 intractable (계산이 불가능)하다.
따라서 아래와 같이 q를 \( \phi \) 로 파라미터화 한뒤 \( p_\theta(z|x) \)에 근사시키려고 한다. 어떻게 근사할수있을지는 다음 lecture에서 이어진다.
답글 남기기
댓글을 달기 위해서는 로그인해야합니다.