[Generative Artificial Intelligence] Latent Variable Models – 2

Stanford CS236 Deep Generative Models 수업의 자료를 기반으로 생성모델의 기본 개념들을 정리해보고자 한다. (참고 https://deepgenerativemodels.github.io/syllabus.html)

지난 lecture에서 마지막 내용은 \( q_\phi (z) \)를 \( p_\theta (x|z) \)에 근사시키면 된다는 이야기였고 이제 이걸 어떻게 근사시킬까 하는 내용이 나온다. 이를 위해 \( log p_\theta (x) \)를 지난 lecture에서 나온 ELBO와 KL divergence식을 통해 표현하는 과정을 한번 더 봐보자

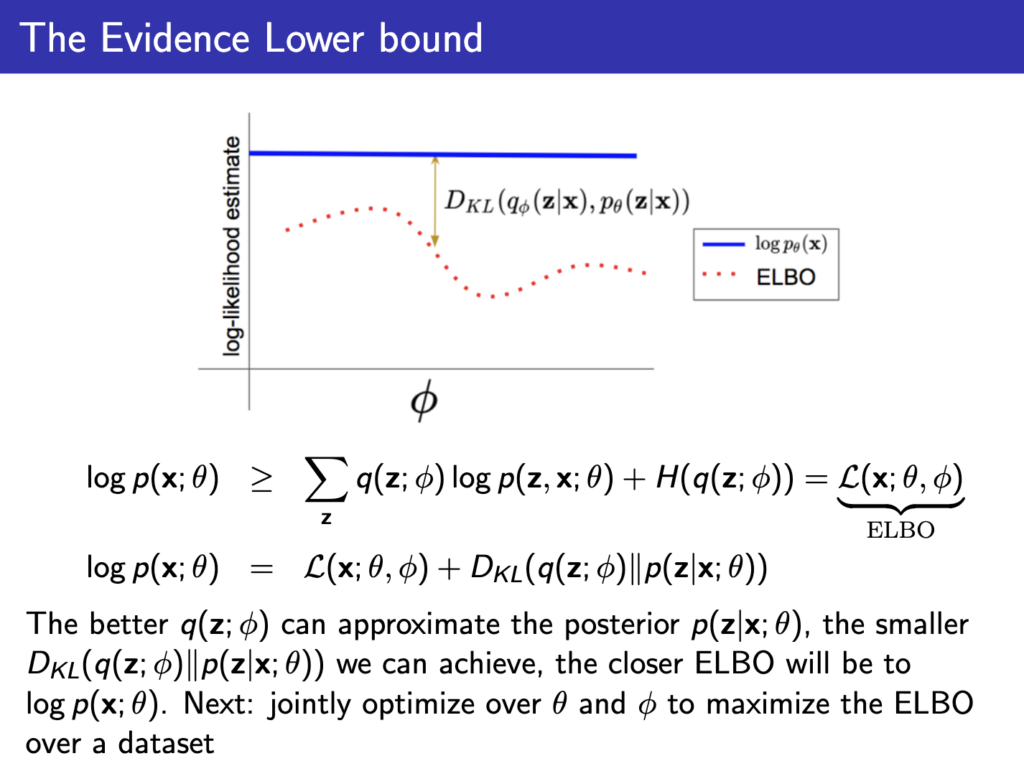
즉 \( q_\phi (z) \)가 \( p_\theta (x|z) \)와 유사해져서 ELBO값이 커지고 KL divergence가 작아지면 작아질수록 ELBO값이 \( log p_\theta (x) \)와 유사해진다!

아래 그림을 보면 이해가 빠른데 ELBO값을 최대화 하는 \( \phi \)를 찾아서 marginal loglikelohood를 근사하고, 그 loss값을 이용해 \( \theta \) 값을 최적화해 \( L(\theta) \)를 최적화하는 variational leraning 방법이 나오게 된다.

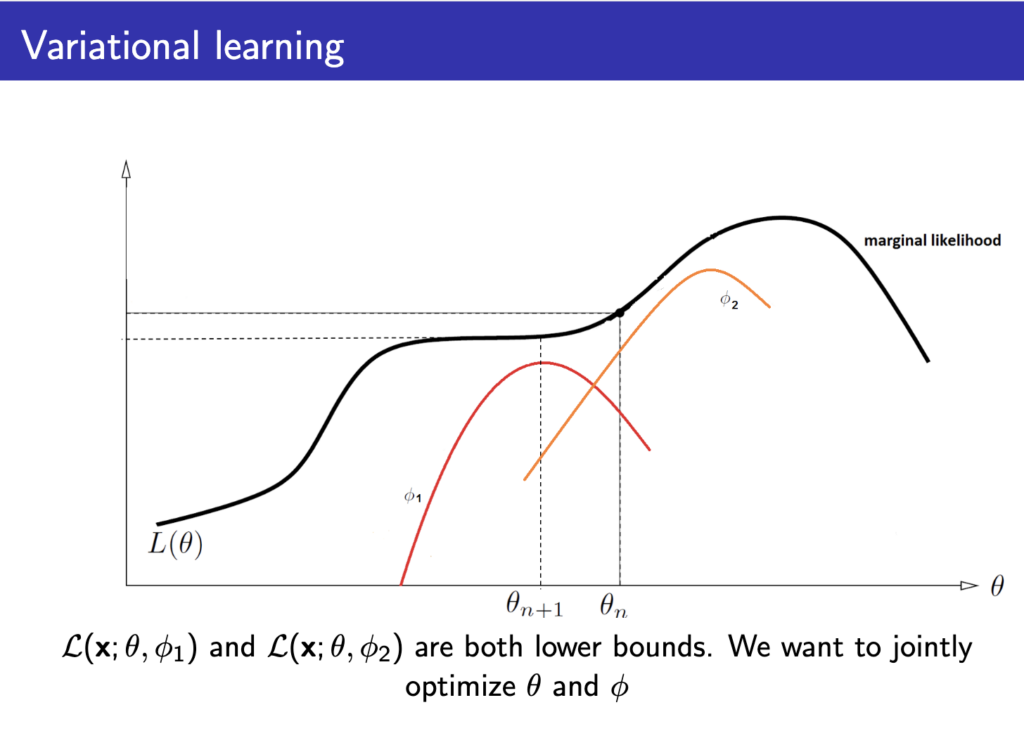
이를 위해 아래와 같은 과정으로 진행한다.

요약하면

1. parameter 초기화
2. 데이터셋 D에서 sample을 k개 추출
3. \( \phi \) 파라미터를 ELBO식에 대해 gradient를 구해 ELBO값을 최대화하는 방향으로 업데이트
4. 위에서 구한 \( \phi \)를 대입해 최종 ELBO식을 구한뒤 이를 최대화 하는 방향으로 \( \theta \)를 업데이트.
5. 다시 2번부터 반복

ELBO식을 최대화하기 위해 gradient를 측정하는 방법은 Monte Carlo 방식을 이용해서 z를 q로부터 sampling해 아래와 같이 gradinet를 구한다.

\( \theta \)의 gradient를 구하는건 위의 식처럼 쉽게 구해지는데, \( \phi \)는 구하기가 조금 복잡하다. 아래처럼 reparameterization 방법을 써서 구할수 있긴 한데 z에 대한 가정을 넣어서 푸는거라 완전 general한 방법은 아니라고 한다.

여튼 이렇게 \( \phi \)의 gradient를 구해 업데이트해서 최적의 \( \phi \)를 구하고 \( \theta \)를 업데이트하는 과정과 반복해서 joint optimization을 진행하면 결국 latent variable model을 얻게 되는거고 \( q_\phi(z|x) \)를 통해 latent를 얻을수도 있고 \( p_\theta(x|z) \)를 통해 latent에서 새로운 데이터 x를 생성할수도 있게 된다.